Efficient offline search evaluation

Offline search evaluation measures search quality using test collections, as opposed to online, where user data such as clicks are used.

Offline search evaluation is important even if user data is available, for the following reasons:

  1. it is more repeatable and can be implemented as automated tests for the system.
  2. it can be more effective than online metrics, depending on the domain (Chen et al.1 find that offline metrics outperform in homogeneous search).
  3. it can be more easily compared between different systems.

As an industry example, a product like Semantic Scholar, although having extensive user data, utilizes a curated test set2 of 250 queries and custom evaluation criteria.

In research literature, test collections e.g. for TREC4 are typically combined from ranked outputs of different systems down to some depth d, before presenting to assessors in random order for judging. Binary relevance, where a document is either judged relevant or not relevant, is usually the main assessment scale. This corresponds well to Q&A systems where a document either contains the answer or it does not, but may not be accurate for systems with a nuanced interpretation of correctness/quality.
In most research evaluations, non-judged documents are deemed as non-relevant, which may result in overpenalization of retrieval methods that rank non-judged but relevant documents highly.

Most industry focused search systems today do not have out of the box support for offline search evaluation, especially in test collection creation and management, and need to be supplemented with libraries such as this5. In Elasticsearch, inbuilt functionality only covers the metrics calculation aspect in the form of the ranking evaluation API6, which assumes a set of test queries and aggregated judgments at hand. Algolia does not have a search evaluation module but instead bundles relevance optimization as a personalization product7.

Key challenges in adapting offline evaluation systems to production environments are

  1. the lack of an efficient framework for test collection creation, management and evaluation.
  2. the application of appropriate metrics to a dynamic dataset whose results may change significantly with time.

To address both challenges, one approach is to apply active ranking with pairwise comparisons, and use partial relevance metrics to measure the results.

For each query in the test set, one or more assessors perform pairwise comparisons between samples drawn from a subset of the document set; active ranking optimizes the comparison sequence by selecting the best pair/s in every iteration. The stopping criteria can be strict ordering, or iteration threshold, or some human judgment or quality measure in the computed ranking. Using the computed ranking, partial relevance metrics are calculated and the comparison history saved. In subsequent evaluations, we can reuse the comparison history, perform new judgments on new documents, and update the ranking and relevance metrics.

Active ranking with pairwise comparisons

For full evaluation the assessor has to judge n items at the same time, which is especially taxing with large n and when each item cannot be judged at a glance. By allowing the user to choose which of 2 items is more relevant, compared to producing an ordered list, cognitive load and decision fatigue is reduced.
In addition, pairwise comparison decouple the final rating scale from the ordering; the same list of comparison outcomes can be used to fit different rating scales. Note that if binary relevance is the objective, pairwise comparison is not necessary since each item is either relevant or not, and can be judged independently.
Other forms of comparisons include Best-Worst Scaling, which presents 3 items and asks the user to choose the best and the worst among the 3. Here I focus on pairwise comparison only.

Pairwise comparison is applied in many real-world scenarios - competitive rankings, surveys, economics, and is closely related to the field of psychometrics. One well known rating system, the ELO rating system, applies pairwise comparison in the context of win, lose or draw outcomes, that updates player ratings in a pool, where the difference in player ratings is a predictor of the outcome of the match.

Different contexts generate different representations of the ranking problem. Some representations include:

For more detailed discussion on these topics, refer to references 8 to 12.

In ranking for search evaluation, we want a solution that can scale easily for 1 assessor or more, minimizes the number of comparisons needed, and ideally has a randomized sequence so that the assessor/s do not keep comparing the same item.
We do not need an absolute ranking result, an approximate one is sufficient, since in the calculation of relevance even fine-grained evaluation often only uses up to 5 point scales.
On the criteria of minimum number of comparisons, an nlogn sorting solution would require an average of 147 comparisons for depth 30, far too many unless we have a large pool of assessors.

ASAP

In this post I will explore the usage of ASAP13 (https://github.com/gfxdisp/asap). Other open source libraries that can also be applied to this problem include choix, Propagon, and milp ranker.

ASAP is a Bayesian approach based on Thurstone’s model (a stochastic transitivity model); it optimizes active sampling by computing the posterior distribution over scores (where scores are the measurements underlying the ranking) from each possible outcome in the next pairwise comparison, and chooses the next comparison based on maximum information gain. Here information gain is calculated as the Kullback-Leibler divergence (a statistical distance metric) between prior and posterior distributions.
To optimize computation, it applies various techniques, including factor graph and expectation propagation inspired by TrueSkill14 (a ranking system developed by Microsoft for Xbox game matchmaking), selective evaluations based on score difference, and a GPU based implementation.

Here’s an example. We start with a concrete representation of the comparison space - a pairwise comparison matrix. For n items, we have an n x n matrix M. To note:

An example initialization is:

[[0 1 1 1 1]
 [1 0 1 1 1]
 [1 1 0 1 1]
 [1 1 1 0 1]
 [1 1 1 1 0]]

We can run ASAP on this initial state or just pick a comparison at random. Assuming we make an initial comparison for M[1][4], and 4 is preferred, the matrix state is now:

[[0 1 1 1 1]
 [1 0 1 1 2]
 [1 1 0 1 1]
 [1 1 1 0 1]
 [1 1 1 1 0]]

Now if we run ASAP on this matrix state, the algorithm then computes the next best pairs with highest information gain, and also outputs the current score with mean and standard deviation. The score mean can be used as a point estimate of the rating of the item in the final ordering, and the standard deviation represents the uncertainty in the estimate of the score.
Assuming our stopping threshold is strict ordering with some threshold difference k, if the threshold difference is not met, we can prompt the next best pairs to the users, get the result, update the matrix state, and run the evaluation again.

Ideas on minimizing judgments

Matrix initialization

Samples drawn from the document set are usually based on an initial ranking formula. We can use a baseline system like BM25 to fetch the initial list, or some combination including our system under test. In that case the initial list is already approximately sorted to some degree. We can express this in terms of the pairwise matrix by this representation:

[[0 2 1 1 1]
 [1 0 2 1 1]
 [1 1 0 2 1]
 [1 1 1 0 2]
 [1 1 1 1 0]]

This is equivalent to preset judgements between every consecutive pair, and a minimally connected graph of M. We can also represent the approximate ranking by anchoring it on some item, e.g. first or last, as in:

[[0 2 3 4 5]                  [[0 1 1 1 5]
 [1 0 1 1 1]                   [1 0 1 1 4]
 [1 1 0 1 1]                   [1 1 0 1 3]
 [1 1 1 0 1]                   [1 1 1 0 2]
 [1 1 1 1 0]]        or        [1 1 1 1 0]]

However these representations are less stable for subsequent updates and have a high degree of error if the anchored item is actually not in the right position as assumed.

One point to note is if we initialize in this way, running ASAP in the first pass may already succeed our stopping criteria, so we need to fix some base number of comparisons first. For example, we may fix n/2 comparisons at the start such that the assessor has seen each document at least once.

Depth of evaluation

Typically when we evaluate the ranking up to depth d, all documents from 1 to d are sampled. However, since we assume the initial distribution has some approximate ordering, there is increasing confidence that documents at depth d and d+1 are interchangeable. That means we can sample less as depth increases, e.g. select all documents from 1-10, 8 from 11-20, 6 from 21-30, etc. to construct the list to be evaluated. This also relies on the assumption that partial relevance metrics are used, which can better handle missing potentially valuable documents.

Weight of comparison

With many assessors, we have many comparisons for the same item to stabilize the ranking, and each assessor needs to perform less comparisons in total. With a single assessor however, more comparisons are needed in order to get a clear strict ordering, depending on our stopping criteria. By adjusting the weights (i.e. points awarded for each M[i][j] comparison) dynamically depending on the number of assessors for the particular round, we can reduce the number of comparisons for all conditions. When the conditions change for subsequent evaluation rounds, we can recompute the rankings objectively since the comparison history is separate from the weights parameter.

Using the above ideas, I average 38 comparisons (median of 35 and max of 75) for a single assessor for 50 test queries at 24 samples each, up to depth 30. In comparison, a nlogn sorting solution would require on average 110 comparisons for 24 samples.

Partial relevance metrics

With the computed rankings, the next step is to calculate metrics that are suitable for incomplete collections.
IR metrics libraries are widely available from the research community. trec_eval (https://github.com/usnistgov/trec_eval) is an evaluation measures library provided by NIST that is the standard tool for computing results reported at TREC. ir-measures (https://ir-measur.es/en/latest/measures.html) is another library that integrates multiple evaluation tools into 1 interface.

For partial relevance, the focus is on which metrics can still reflect user preference accurately in the presence of missing judgments. Sakai and Kando16 apply 2 measures to this: discriminative power, defined as the proportion of system pairs with a statistically significant difference for a given probability of Type 1 Error, and Kendall’s rank correlation, and claim that Q’, nDCG’ and AP’ are superior to bpref and Rank Biased Precision (RBP). Here I focus on bpref and nDCG'.

bpref was proposed by Buckley and Voorhees17 in 2004, and used in TREC judgments soon after, but not much in recent tracks. bpref is highly correlated with mean average precision when full relevance assessments are available.
An explanation of bpref is that it scores each judged, relevant document adjusted by the number of judged, non-relevant documents above it. The definition is as follows (from trec_eval bpref code): $$bpref = \frac{1}{R}\sum_{r}(1-\frac{\mathrm{min}(R,n')}{\mathrm{min}(R,N)})$$ where R is the number of judged relevant documents, N is the number of judged non-relevant documents, r is a relevant retrieved document, and n’ is the number of judged non-relevant documents ranked above r.

nDCG’ as defined by Sakai and Kando is simply the original measure applied to a condensed list, i.e. removing all unjudged documents from the list.
nDCG is calculated by dividing DCG with iDCG - the ideal ordering of documents sorted by relevance; this ideal ordering can be represented by our computed ranking in the previous step. In DCG, judgements are on a graded scale and adjusted by the logarithm of the document position. Removing unjudged documents means that the document position is unaffected by a change in unjudged documents.
There are a number of configurable parameters which affect the calculation of DCG, primarily the exponentiation of the relevance gain and the selection of the logarithm base: $$DCG = \sum_{i=1}\frac{rel_i}{\mathrm{log_x}(i\,+\,1)}$$ where reli is usually either the graded score of the document at i or 2 raised to the power of the graded score, and x is usually 2 or a small positive real number. In general the default parameters are no exponentiation and a logarithm of base 2.

From the computed rankings in the previous section, we can easily adapt to different evaluation measures. In the case of bpref, we just need to identify the decision boundary for relevant / non relevant, i.e. the position at which the current document is relevant and the next document is not relevant. In the case of nDCG’, we can manually identify the decision boundary for each grade in the scale, or segment automatically by dividing the grades evenly across the relevant documents.
When new documents are added or removed, we can regenerate the ranking based on the updated comparison history, and check those decision boundaries that were changed i.e. where the adjacent documents are different from before.

System design

In conclusion, the complete system looks like this:

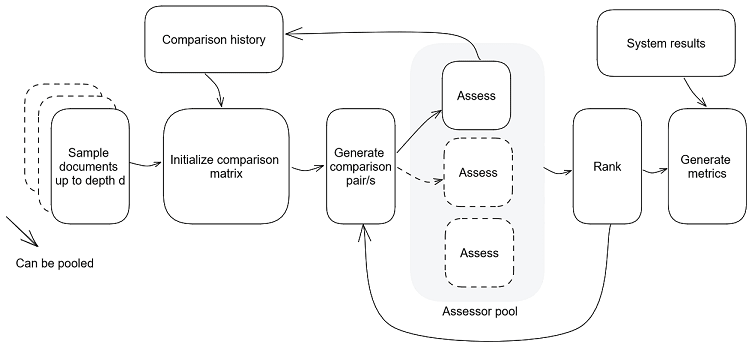
Offline search evaluation system design
Evaluation round for 1 test query

We gather an initial candidate list to evaluate. If there are historical comparisons, we can integrate them into the initialization process, otherwise, we may choose different parameters for first time evaluation. Next, we generate comparison pairs that are optimal for the current state. If the approach we are using allows batch generation (ASAP has a batch mode), we can distribute different pairs to different assessors; otherwise, we may choose to distribute the same pair for all assessors.
Choices made by the assessor/s are recorded into the comparison history. Depending on how ‘realtime’ our evaluation process is, we may choose to rank after every comparison or after aggregating a set of comparisons. Based on the ranking stopping criteria, we either continue to generate more pairs, or complete the evaluation for this round.
The computed ranking can then be used to generate relevance metrics for the system under test. We can compare the change in system quality by measuring statistical differences in relevance metrics across all test queries.



References

  1. Chen, Ye et al. “Meta-evaluation of Online and Offline Web Search Evaluation Metrics.” Proceedings of the 40th International ACM SIGIR Conference on Research and Development in Information Retrieval (2017)
  2. https://blog.allenai.org/building-a-better-search-engine-for-semantic-scholar-ea23a0b661e7
  3. Büttcher, Stefan, Charles L. A. Clarke, and Gordon V. Cormack. Information Retrieval: Implementing and Evaluating Search Engines. Cambridge, Mass: MIT Press, 2010. Print.
  4. https://trec.nist.gov/
  5. https://sease.io/2021/01/offline-search-quality-evaluation-rated-ranking-evaluator-rre.html
  6. https://www.elastic.co/guide/en/elasticsearch/reference/current/search-rank-eval.html
  7. https://www.algolia.com/blog/product/what-is-search-relevance/
  8. Maystre, Lucas and Matthias Grossglauser. “Just Sort It! A Simple and Effective Approach to Active Preference Learning.” ICML (2017)
  9. Shah, Nihar B. and Martin J. Wainwright. “Simple, Robust and Optimal Ranking from Pairwise Comparisons.” ArXiv abs/1512.08949 (2017)
  10. Heckel, Reinhard et al. “Active ranking from pairwise comparisons and when parametric assumptions do not help.” arXiv: Learning (2016)
  11. Szörényi, Balázs et al. “Online Rank Elicitation for Plackett-Luce: A Dueling Bandits Approach.” NIPS (2015)
  12. Dushkin, Eyal and Tova Milo. “Top-k Sorting Under Partial Order Information.” Proceedings of the 2018 International Conference on Management of Data (2018)
  13. Mikhailiuk, Aliaksei et al. “Active Sampling for Pairwise Comparisons via Approximate Message Passing and Information Gain Maximization.” 2020 25th International Conference on Pattern Recognition (ICPR) (2021): 2559-2566.
  14. https://www.microsoft.com/en-us/research/wp-content/uploads/2007/01/NIPS2006_0688.pdf
  15. https://www.microsoft.com/en-us/research/uploads/prod/2018/03/trueskill2.pdf
  16. Sakai, Tetsuya and N. Kando. “On information retrieval metrics designed for evaluation with incomplete relevance assessments.” Information Retrieval 11 (2008): 447-470.
  17. Buckley, Chris and Ellen M. Voorhees. “Retrieval evaluation with incomplete information.” SIGIR ‘04 (2004)